本文目录导读:
铅锤的原理和铅锤公式可以通过面积法来证明,下面将详细介绍这一过程。
铅锤的原理
铅锤的原理主要涉及到物理中的重力作用和力矩平衡,铅锤是一种利用重力方向总是竖直向下的原理制作的简单仪器,它可以帮助我们找到重力方向,从而确定某个物体是否垂直。
铅锤公式的表述
铅锤公式通常用来描述与铅锤相关的几何关系,在三角形中的应用,可以通过公式计算出三角形的某些属性。
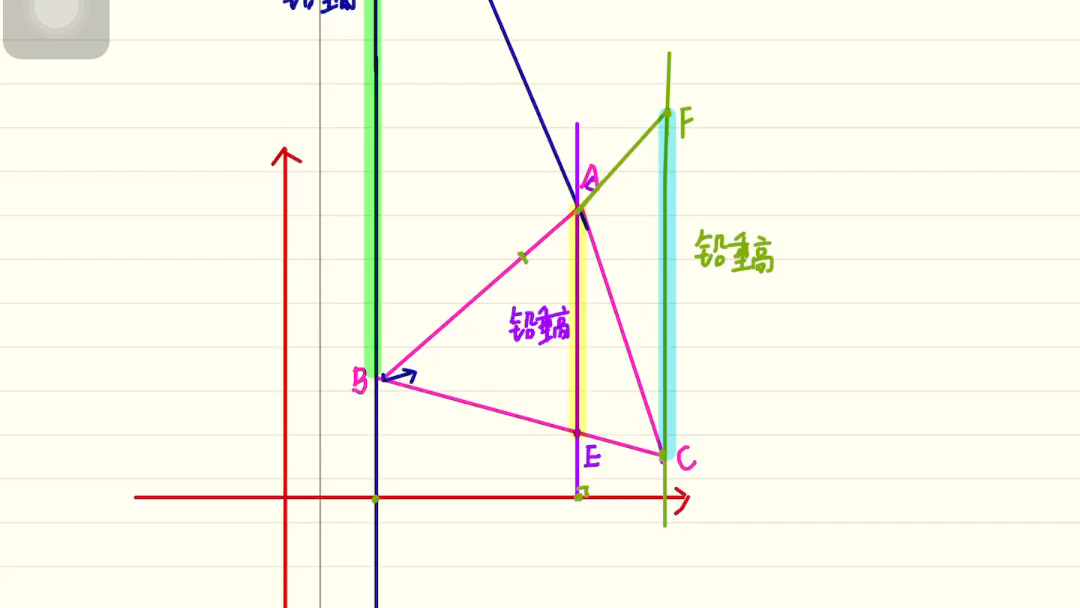
使用面积法证明铅锤公式
面积法是一种几何证明方法,通过计算图形的面积来验证定理或公式,以下是使用面积法证明铅锤公式的一般步骤:
1、设定问题并明确要证明的铅锤公式。
2、根据铅锤的原理和几何知识,画出与问题相关的图形。
3、通过计算图形的面积,并结合已知条件和图形关系,推导出要证明的公式。
4、确保推导过程严密、逻辑清晰,得出最终结论。

具体证明过程(以三角形为例)
1、假设我们有一个三角形,其中一角悬挂铅锤,我们可以利用铅锤的位置来证明三角形的某些性质。
2、通过观察图形,我们可以发现铅锤所在的直线与三角形的某一边相交,将三角形分为两部分。
3、通过计算这两部分的面积,并结合三角形的性质,我们可以推导出与铅锤相关的公式,如果这两部分面积相等,那么我们可以证明三角形是等腰三角形。
通过以上步骤,我们可以使用面积法证明铅锤公式,这种方法帮助我们更直观地理解铅锤的原理和几何关系,从而加深对相关知识的理解和应用。
 TIME
TIME
